Seja
![]() um difeomorfismo
um difeomorfismo ![]() numa vizinhança da esfera
numa vizinhança da esfera ![]() e
e ![]() a superfície imagem de
a superfície imagem de ![]() por
por ![]() , ou seja,
, ou seja,
![]() .
.
Podemos parametrizar ![]() com duas cartas:
com duas cartas:
![]() e
e
![]() , onde
, onde
![]() e
e
![]() são dadas por projeção estereográfica:
são dadas por projeção estereográfica:
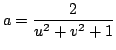 ,
,
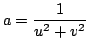 ,
,
A notação acima é para explicitar qual polo de ![]() (relativo à terceira coordenada) é coberto pela carta, ou seja,
(relativo à terceira coordenada) é coberto pela carta, ou seja,
![]() e
e
![]() .
.
Usando estas informações, podemos parametrizar ![]() com duas cartas
com duas cartas
![]() e
e
![]() , onde
, onde
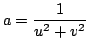 ,
,