Primeiramente fixamos a orientação de ![]() dada pelo vetor que aponta para fora de
dada pelo vetor que aponta para fora de ![]() . Fixamos um ponto
. Fixamos um ponto ![]() em
em ![]() , definimos esse ponto como vértice da triangulação. Fixamos uma direção no plano tangente a
, definimos esse ponto como vértice da triangulação. Fixamos uma direção no plano tangente a ![]() em
em ![]() e traçamos uma aresta partindo desse ponto com medida
e traçamos uma aresta partindo desse ponto com medida ![]() , isso é possível pela solução do Problema 1. Obtemos assim, um ponto
, isso é possível pela solução do Problema 1. Obtemos assim, um ponto ![]() que também será um vértice da triangulação. Encontramos um ponto
que também será um vértice da triangulação. Encontramos um ponto ![]() tal que
tal que ![]() ,
,![]() ,
,![]() sejam vértices de um triângulo equilátero e a poligonal fechada orientada
sejam vértices de um triângulo equilátero e a poligonal fechada orientada
![]() tenha a orientação induzida pela orientação de
tenha a orientação induzida pela orientação de ![]() dada pelo vetor que aponta para fora de
dada pelo vetor que aponta para fora de ![]() com origem em um ponto qualquer no interior do triangulo
com origem em um ponto qualquer no interior do triangulo
![]() . Essa poligonal divide
. Essa poligonal divide ![]() em duas regiões: uma triangulada e outra não. Ressaltamos que a orientação da poligonal é invertida se tormarmos como origem do vetor que aponta para fora de
em duas regiões: uma triangulada e outra não. Ressaltamos que a orientação da poligonal é invertida se tormarmos como origem do vetor que aponta para fora de ![]() um ponto fora da área triangula de
um ponto fora da área triangula de ![]() . Fazemos então iterações sucessivas na área triangulada acrescentando um novo triângulo a esta a cada iteração, de forma que a nova área triangulada de
. Fazemos então iterações sucessivas na área triangulada acrescentando um novo triângulo a esta a cada iteração, de forma que a nova área triangulada de ![]() seja conexa e não degenerada, ou seja, pelo menos uma das arestas do triângulo acrescentado deve ser uma aresta do bordo da área triangulada de
seja conexa e não degenerada, ou seja, pelo menos uma das arestas do triângulo acrescentado deve ser uma aresta do bordo da área triangulada de ![]() obtida na iteração anterior e esse triângulo esteja contido na área não triangulada de
obtida na iteração anterior e esse triângulo esteja contido na área não triangulada de ![]() . Se todos os triângulos adicionados tiverem áreas aproximadamente iguais então, visto que
. Se todos os triângulos adicionados tiverem áreas aproximadamente iguais então, visto que ![]() tem área finita, após um número finito de iterações obteremos a triangulação desejada.
tem área finita, após um número finito de iterações obteremos a triangulação desejada.
Visto que o bordo da área triangulada de cada iteração contém pelo menos uma aresta do próximo triângulo a ser adicionado, podemos estabelecer um controle da triangulação fazendo com que todas as arestas desse bordo tenha o mesmo comprimento, sempre que possível.
Seja
![]() uma poligonal fechada simples, orientada no sentido anti-horário. Essa poligonal limita duas regiões conexas do plano: uma região interior e uma região exterior a
uma poligonal fechada simples, orientada no sentido anti-horário. Essa poligonal limita duas regiões conexas do plano: uma região interior e uma região exterior a ![]() . Seja
. Seja
![]() uma função de classe
uma função de classe ![]() injetiva e que omite apenas um ponto. A poligonal
injetiva e que omite apenas um ponto. A poligonal
![]() , obtida ligando-se a imagem dos
, obtida ligando-se a imagem dos ![]() 's por segmentos de reta na mesma ordem em que os
's por segmentos de reta na mesma ordem em que os ![]() 's são ligados em
's são ligados em ![]() , divide
, divide ![]() em duas regiões conexas que identificaremos como interior e exterior a
em duas regiões conexas que identificaremos como interior e exterior a
![]() conforme seja imagem da região interior ou exterior a
conforme seja imagem da região interior ou exterior a ![]() em
em
![]() (o ponto omitido pertencerá à região exterior a
(o ponto omitido pertencerá à região exterior a
![]() ). Essa definição permite-nos falar em ângulo externo e interno nos vértices de
). Essa definição permite-nos falar em ângulo externo e interno nos vértices de ![]() e
e
![]() , Veja a Figura 2.
, Veja a Figura 2.
Denotamos por ![]() o ponto imagem
o ponto imagem
![]() . Suponha que o ângulo externo em
. Suponha que o ângulo externo em ![]() seja
seja ![]() e que o ângulo externo em
e que o ângulo externo em ![]() seja
seja ![]() .
.
Problema 2:
Dados
![]() compatível com a geometria de
compatível com a geometria de ![]() ,
,
![]() com
com
![]() , encontrar
, encontrar
![]() um ponto na região exterior a
um ponto na região exterior a ![]() tal que se
tal que se
![]() então
então
![]() e o ângulo medido na região exterior a
e o ângulo medido na região exterior a
![]() , medido na orientação de
, medido na orientação de ![]() entre os vetores
entre os vetores
![]() e
e
![]() seja
seja ![]() .
.
Problema 3:
Seja
![]() . Dado
. Dado
![]() , encontrar
, encontrar
![]() um ponto na região exterior a
um ponto na região exterior a ![]() tal que
tal que
![]() ou
ou
![]() (preferenciamente ambos) e os ângulos medido na região exterior a
(preferenciamente ambos) e os ângulos medido na região exterior a
![]() na orientação de
na orientação de ![]() entre os vetores
entre os vetores
![]() e
e
![]() e entre os vetores
e entre os vetores
![]() e
e
![]() sejam iguais.
sejam iguais.
De posse da solução destes dois problemas podemos obter a triangulação desejada. De fato, após o cálculo dos três primeiros vértices, a cada nova iteração, é possível que um dos casos abaixo aconteçam, então resolvemos eles na mesma ordem de prioridade quem aparecem abaixo:
Caso 1: Um dos ângulos externos a
![]() é menor que
é menor que ![]() . Veja a Figura 3.
. Veja a Figura 3.
Suponha que isso ocorra em um vértice genérico ![]() . Nesse caso inserimos na triangulação o triângulo
. Nesse caso inserimos na triangulação o triângulo
![]() , então o ponto
, então o ponto ![]() deixará de fazer parte do bordo da área triangulada, assim como as aresta que eram adjacentes a ele,
ou seja,
deixará de fazer parte do bordo da área triangulada, assim como as aresta que eram adjacentes a ele,
ou seja,
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() .
.
Caso 2: Existe uma aresta de
![]() de comprimento
de comprimento ![]() , (por exemplo: arestas geradas no Caso 1). Veja a Figura 4.
, (por exemplo: arestas geradas no Caso 1). Veja a Figura 4.
Seja
![]() essa aresta. Nesse caso usamos a solução do Problema 2 e encontramos
essa aresta. Nesse caso usamos a solução do Problema 2 e encontramos
![]() exterior a
exterior a ![]() tal que
tal que
![]() e
e
![]() , nesse caso obteremos
, nesse caso obteremos
![]() . Se existe algum vértice de
. Se existe algum vértice de
![]() não-adjacente a
não-adjacente a ![]() cuja distância a
cuja distância a ![]() é menor que
é menor que ![]() passamos ao Caso 4, caso contrário, inserimos na triangulação o triângulo
passamos ao Caso 4, caso contrário, inserimos na triangulação o triângulo
![]() e
e
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() . Se após essa iteração o novo ângulo externo em
. Se após essa iteração o novo ângulo externo em ![]() for menor que
for menor que ![]() , desfazemos a iteração e passamos ao Caso 3 abaixo.
, desfazemos a iteração e passamos ao Caso 3 abaixo.
Caso 3: Seja ![]() um vértice de
um vértice de
![]() a partir do qual é possível inserir uma aresta de lado
a partir do qual é possível inserir uma aresta de lado ![]() mas essa aresta divide o ângulo externo de
mas essa aresta divide o ângulo externo de ![]() em dois ângulos cuja soma é menor que
em dois ângulos cuja soma é menor que ![]() . Veja a Figura 5.
. Veja a Figura 5.
Nesse caso usamos a solução do Problema 3. Encontramos
![]() exterior a
exterior a ![]() tal que
tal que
![]() divida o ângulo externo de
divida o ângulo externo de ![]() em dois ângulos iguais e
em dois ângulos iguais e
![]() . Se
. Se
![]() então teremos, também,
então teremos, também,
![]() . Se a aresta inserida dividir o ângulo externo de
. Se a aresta inserida dividir o ângulo externo de ![]() em dois ângulos menores que
em dois ângulos menores que ![]() , então inserimos na triangulação o triângulo
, então inserimos na triangulação o triângulo
![]() e
e
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() . Se existe algum vértice de
. Se existe algum vértice de
![]() não-adjacente a
não-adjacente a ![]() cuja distância a
cuja distância a ![]() é menor que
é menor que ![]() passamos ao Caso 4, caso contrário inserimos na triangulação os triângulos
passamos ao Caso 4, caso contrário inserimos na triangulação os triângulos
![]() e
e
![]() e
e
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() .
.
Caso 4: Existe um vértice em
![]() , a partir do qual não é possível inserir uma nova aresta de comprimento
, a partir do qual não é possível inserir uma nova aresta de comprimento ![]() (isso acontece, por exemplo, nos últimos passos da triangulação). Veja a Figura 6.
(isso acontece, por exemplo, nos últimos passos da triangulação). Veja a Figura 6.
Se o ângulo em ![]() ou em
ou em ![]() ou em
ou em ![]() for menor que
for menor que ![]() , tomamos aquele que tem o menor ângulo, que, sem perda de generalidade podemos supor que este seja
, tomamos aquele que tem o menor ângulo, que, sem perda de generalidade podemos supor que este seja ![]() , então inserimos na triangulação o triângulo
, então inserimos na triangulação o triângulo
![]() e
e
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() (note que se o ângulo escolhido fosse
(note que se o ângulo escolhido fosse ![]() ou
ou ![]() a operação acima também afetaria o ângulo externo em
a operação acima também afetaria o ângulo externo em ![]() ). Se não tivermos a propriedade acima usamos a solução do Problema 1 e inserimos a partir de
). Se não tivermos a propriedade acima usamos a solução do Problema 1 e inserimos a partir de ![]() uma aresta cujo comprimento seja a metade da menor distância entre
uma aresta cujo comprimento seja a metade da menor distância entre ![]() e os outros vértices não-adjacentes a ele usando a mesma regra que foi usada no Caso 2 em relação ao ângulo e finalizamos, também, como no Caso 2. Se o ângulo externo em
e os outros vértices não-adjacentes a ele usando a mesma regra que foi usada no Caso 2 em relação ao ângulo e finalizamos, também, como no Caso 2. Se o ângulo externo em ![]() for como no Caso 3, inserimos uma aresta com o comprimento descrito acima de forma que divida esse ângulo em dois ângulos iguais e finalizamos como no Caso 3.
for como no Caso 3, inserimos uma aresta com o comprimento descrito acima de forma que divida esse ângulo em dois ângulos iguais e finalizamos como no Caso 3.
Caso 5: Se nenhum dos casos acima ocorrem.
Escolhemos um vértice ![]() de
de
![]() . Calculamos
. Calculamos
![]() exterior à
exterior à ![]() de forma que o triângulo
de forma que o triângulo
![]() seja equilátero. Incluimos esse triângulo na triangulação e então
seja equilátero. Incluimos esse triângulo na triangulação e então
![]() deixa de ser
deixa de ser
![]() e passa a ser
e passa a ser
![]() .
.
Solução do Problema 2:
Seja ![]() o ângulo externo a
o ângulo externo a
![]() . Pela solução do Problema 1, para todo
. Pela solução do Problema 1, para todo
![]() encontramos
encontramos
![]() exterior a
exterior a ![]() tal que o ângulo entre
tal que o ângulo entre
![]() e
e
![]() seja
seja ![]() e tal que
e tal que
![]() . Temos, portanto, bem definidas, as funções
. Temos, portanto, bem definidas, as funções
![]() e
e
![]() , onde
, onde ![]() é o ângulo externo a
é o ângulo externo a ![]() em
em
![]() , dadas por
, dadas por
![]() e
e
![]() , onde
, onde
![]() denota o ângulo entre dois vetores, medido na orientação de S (Nota:
denota o ângulo entre dois vetores, medido na orientação de S (Nota: ![]() e
e
![]() tem a mesma classe de diferenciabilidade de
tem a mesma classe de diferenciabilidade de ![]() ).
).
Para resolvermos este problema o ideal seria procedermos como na solução do Problema 1, aplicando o Método de Newton à função ![]() , mas
, mas ![]() aparesce de forma implicita, tornando esta opção um pouco complicada devido à necessidade dos valores da derivada de
aparesce de forma implicita, tornando esta opção um pouco complicada devido à necessidade dos valores da derivada de ![]() . Em vez disto, optamos por um método alternativo, similar ao Método de Newton, usando o fato de que
. Em vez disto, optamos por um método alternativo, similar ao Método de Newton, usando o fato de que ![]() é estritamente crescente e tem domínio e imagem limitados.
é estritamente crescente e tem domínio e imagem limitados.
Primeiro escolhemos um valor inicial para ![]() , então executamos o algoritmo descrito abaixo:
, então executamos o algoritmo descrito abaixo:
![]() ;
;
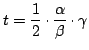 ;
;
![]() ;
;
![]() ;
;
while(
![]() )
)
{
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
} return ![]() ;
;
Aqui, a função ``clamp ''é definida por:
![]() ;
;
O ponto desejado é, então, o ponto ![]() obtido na solução do Problema 1.
obtido na solução do Problema 1.
Solução do Problema 3:
O algoritmo que usamos para resolver este problema é similar ao que usamos na solução do Problema 2, a diferença é que, neste caso, o comprimento da aresta a ser inserida e o ângulo que esta aresta deve formar com a aresta
![]() são alterados a cada ``loop''do algoritmo. Esse algoritmo é descrito abaixo:
são alterados a cada ``loop''do algoritmo. Esse algoritmo é descrito abaixo:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
while(
![]() )
)
{
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
} return ![]() ;
;
Aqui, ![]() é o comprimento da aresta a ser inserida,
é o comprimento da aresta a ser inserida, ![]() é o ângulo que ela deve formar com a aresta
é o ângulo que ela deve formar com a aresta
![]() e
e ![]() denota o comprimento da aresta
denota o comprimento da aresta
![]() . A função ``
. A função ``
![]() ''retorna o maior entre os números
''retorna o maior entre os números ![]() e
e ![]() . A restrição a
. A restrição a ![]() é para evitar que tenhamos arestas muito grandes.
é para evitar que tenhamos arestas muito grandes.
O ponto desejado é, então, o ponto ![]() obtido na solução do Problema 1.
obtido na solução do Problema 1.