SIBGRAPI 2005
A NOVEL ALGORITHM FOR ACTIVE CONTOUR
MODELS: ADAPTIVE SNAKES
Anderson Marques de Santana, Ruy Alberto Correa Altafim, Adilson Gonzaga,
Abstract. We present
a novel algorithm to optimize deformable contour models. It overcomes an
inherent problem of traditional snakes using a dynamic intervention in the evolution
of the curve so that leads to better fidelity in contour detection. In practice,
the main difference from the traditional GVF snakes is the definition of a feature
merit function. The proposed method solves the problem of points bunching
together on strong portions of the contour and achieves fuller matching of
concavities with external forces. We also show with a set of well-parameterized
images that the proposed solution leads to better convergence and matching.
[ project home page | contact authors ]
1. Introduction
The parametric active
contour model known as snakes was first proposed by Kass
et all [1] and has been widely used in image
processing and computer vision. These models simulate elastic materials which
can fit themselves dynamically to object shapes in response to internal forces,
external image forces, and user-specified constraints. Grasping [2], and tracking [3] are illustrative application examples.
The snake
was originally defined as a curve ![]() ,
, ![]() that evolves through the
spatial domain of the image to minimize an energy function. The snake has been used
widely but its original formulation is inadequate for images with deep
concavities or a complex geometry and topology. These questions have been raised
in recent publications and attempts made to improve these aspects of the
original implementation [4], but they do not achieve a global analysis of the
optimum inter-distance and the problem is only addressed by the insertion of severe
constraints and essentially different formulations [5].
that evolves through the
spatial domain of the image to minimize an energy function. The snake has been used
widely but its original formulation is inadequate for images with deep
concavities or a complex geometry and topology. These questions have been raised
in recent publications and attempts made to improve these aspects of the
original implementation [4], but they do not achieve a global analysis of the
optimum inter-distance and the problem is only addressed by the insertion of severe
constraints and essentially different formulations [5].
The solution
proposed here is an adaptive algorithm that uniquely addresses the problem by a
global analysis of the optimal inter-distance. The results generated show that this
method greatly enhances the contour detection accuracy.
2. Proposed Solution
The proposed principle
of adaptation is the definition of new optimal point positions along the snake
that minimize a morphological energy function ![]() shown in equation
1,
shown in equation
1,
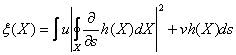 (1)
(1)
where h(X) represents the
merit function, and u and v are weighting factors specified by the user to
balance the differential and the non-differential terms. The merit function is
chosen to have local minima in the regions of interest such that the updated point
positions improve the accuracy in the desired portions of the contour. Equation
2 shows a typical merit function example,
![]() (2)
(2)
where
np is the number of points, is shown in figure 1
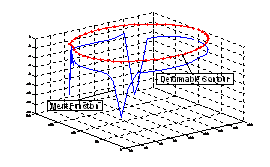
Figure 1 – Merit function (---) and deformable contour (-+-)
3. Experimental Results
For two well-parameterized
synthetic images, figure 2 presents a comparison between the traditional GVF
snakes formulation [6] and the proposed adaptive algorithm for a poor snake (both
with 30 points). As we can see, the proposed algorithm significantly enhances
the contour detection performance.


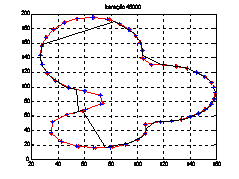
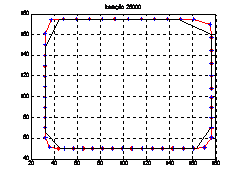
Figure 2- GVF snake (---) and
adaptive snake (-+-): flat/flat image (a) and
curve/curve image (b)
4. Conclusions
The experimental results
show that the proposed algorithm needs fewer points then the traditional snake
formulation and is uniquely able to address the extern force concavity
achieving capability. Its low processing time is also an important aspect to be
considered in image recognition scheme for vision systems.
5. References

[1] M. Kass, A. Witkin
e D. Terzopoulos, “Snakes: active contour
models”, International Journal of Computer Vision, Vol
1, N. 4, 1987.
[2] D. P. Perrin, E.
Kadioglu, S. A. Stoeter and
N. Papanikolopoulos, “Grasping and Tracking
Using Constant Curvature Dynamic Contours”, The International Journal of
Robotics Research, Vol 22, No. 10-11,
October-November 2003.
[3] K. Seo, T. Choi and J. Lee,
“Adaptive Color Snake Model for Real-Time Object Tracking”,
Proceedings of the 2004 IEEE International Conference on Robotics &
Automation, New Orleans, LA, April, 2004.
[4] X. Xie and M. Mirmehdi, “RAGS:
Region-Aided Geometric Snake”, IEEE Transactions on Image Processing,
Vol. 13, No. 5, May 2004.
[5] D. Geiger, A. Gupta, L A. Costa e J Vlontzos, “Dynamic Programming for Detecting, Tracking and Matching Deformable Contours”, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 17, N. 3, Março, 1995.
[6] C. Su, J. L. Prince, “Snakes, Shapes, and Gradient Vector Flow”, IEEE Transactions on Image Processing, Vol. 7, No. 3, March 1998.