Hierarchical 4-K Meshes
Hierarchical 4-K Meshes |

|
|
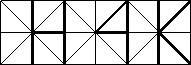
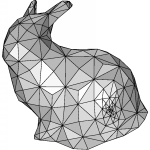
Hierarchical 4-K Meshes constitute a powerful framework for variable-resolution representation of surfaces, as well as, for adaptive computations on 2D manifolds. The framework is integrated by a data structure, together with a set of procedures that operate on it. We have developed methods for constructing 4-K meshes based on subdivision, adaptive refinement, and simplification. We have also implemented operators for mesh extraction, interrogation and conversion to other representations. The figures below illustrate the expressiveness of the 4-K structure. These meshes conform to various adaptation criteria, including: gradual change in resolution; region segmentation; and point location. We used simplification (left) and subdivision (center, right) to generate the underlying hierarchical structures.
|

|

|
|
|
Variable Resolution 4-K Meshes:
This paper describes the variable-resolution 4-K data structure.
It also gives an overview of construction methods, including:
subdivision, refinement and simplification.
|


|
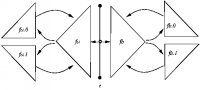
A Unified Approach for Hierarchical Adaptive Tessellation of Surfaces
This paper introduces a method for adaptive tessellation of parametric
and implicit surfaces.
It employs a refinement algorithm that generates hierarchical 4-K meshes.
|

|
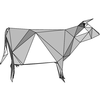
Four-Face Cluster Simplification
This paper presents a simplification algorithm based on edge swaps and
vertex removals that produces a 4-K mesh hierarchy.
|


|
Hierarchical Generalized Triangle Strips
This paper develops a methodology for maintaining a path on a triangulation
under refinement.
|
Last Update: Fri Mar 17 19:20:09 EST 2000 by lvelho.